Python3 でガチャ計算機を作ってみよう

今回は、先日 Pythone3.8.3 をインストールしてから HelloWorld しかやってないので、他にもいろいろ作ってみようのシリーズをやってみたいともいます。

作るにしてもなにか自分のためになるもので、いつも遊んでるスマホアプリでみんな大好きガチャを見える化するための計算機を作ってみたいと思います。

これは、わたしが、ゲームでガチャを引くとき、Excelで一応計算して、今持ってる聖石、夢球、水晶、念石等々でどれくらい回せば出るのかを計算することがあるのですが、せっかくなので、Pythonでそんなアプリを作ってみたいともいます。

とは言っても、HelloWorld の次のアプリなので、とにかく簡単なもので、解説できるようなレベルの簡単なものです。

まずは、ガチャの理屈から

最近のガチャは、きちんと、提供割合というのを示してくれています。

まぁ、ウルトラレアなカードやキャラクターは、0.1%を下回ることをあるほど低確率なので、最初から絶望的な感じで、当たればラッキーくらいに思ってしまいます。

ただ、ここで、ゲームにもよりますが、ガチャを回すためのアイテムがたくさん溜まっているときに、結構無理して引いてしまって、爆死して後悔することがよくあります。このときもある程度計画的に回した方がよいですよね。

よく聞くガチャの確率の話で、当たりが、1% です。となっているガチャは、何回引けば、1回当たるのかという話をしますが、大体100回引いたら1回当たるという感じのことを言う人がいます。まぁ、大体といついているので、間違いとは言えないかもしれませんが、これって正確ではありません。じゃあ、0.1%のウルトラレアって1000回引かないといけないのということになってしまいますが、1000回まわすのにアイテムどんだけ使うんだって思うと最初から引けません。でも、実は1回当たればいいわけですからそれを条件に考えるとそんなに引く必要はありません。もちろん、このガチャは、常にあたり1%となっており、引いたカードは再度箱に戻すというのがルールです。つまり永遠に当たらないこともあり得ますが、確率的には、いずれは当たります。いわゆる 0.9999...(無限に9が続くと)＝1 というやつです。

1回当たるまで何回引くと何%になるかを考えます。つまり、0.1%のガチャを10回ひくのと、100回ひくのでは、少なくとも1回当たる確率というのは違うはずです。たくさん引けば引くほど1回当たる確率は上がっていくはずです。

1回で当たる確率は、0.1% なので、そのまま 0.1% です。

じゃあ、2回で当たる確率は、どうなるでしょう。2回ともはずれる場合の確率を100%から引けば、よいことになります。つまり、当たりを〇、はずれを×としたとき、一度でも〇になればいいのですから、〇〇、〇×、×〇、××、と４つの場合のうち、〇〇、〇×、×〇、の確率を計算するのでは、なく、××となる確率を計算して、１から引くことで残りの場合の確率を出すというように考えます。

では、2回とも外れる確率はとなると、×は、100%-0.1% = 99.9% という確率になるので、2回連続×になるのは、0.999 × 0.999 = 0.0099.800 = 0.998001% になります。つまり2回引いて1回当たる確率は、100% - 99.8001% = 0.1999% になるわけです。2回引くだけで、0.1% → 0.1999% と確率がアップしました。ここで、2%と単純に2倍にならないのか厳しい世界ではあります。

じゃあ、10回引いて1回当たる確率は、ということですが、10回連続外れるのは、99.9%を10回かけて、0.99^10 になるので、99.004 %となり、1回当たる確率は、100%-99.004% = 0.9955% となります。ほぼ1% でしょうか。(ここで、^はべき乗をあらわしています。2の3乗は、2^3 と表します。)

1000回引くと、連続1000回外れは、99.99^1000 = 0.3677 = 36.77 % となります。逆に1回当たる確率は、100%-36.77% = 63.23% となります。63.23%ということは、すでにこの時点で1回は当たっていてもおかしくない確率になっています。逆に1000回連続外す方が難しいということになります。

ここで、確率でよく聞く話で、0.1%のガチャは、1000回回せば1回は当たるんじゃないのという話は大きく異なった結果になっていることがわかります。

1000回回して、全部はずす方が難しいのですから、じゃあ、連続で外す方が難しくなる回し回数は、どのあたりになるかを考えます。

全部外す確率と、1回は当たりが来る確率がちょうど50%、50% になる回数nを求めると、0.1%のガチャは、n回まわして1回当たる方が、n回外すよりも簡単になるという回数があるはずです。

では、当たる確率を 50%をちょうど超える回数を求めたいと思います。これをガチャ計算機の回数としてももとめる機能にします。つまり、ウルトラレアの確率を入れたら、50%を超える回数を求める計算機ということです。

ウルトラレアの確率を x % とします。

連続 n 回外す確率は、(1-x/100) ^ n となるため、少なくとも1回当たる確率は、

で表すことができます。

この値が、50% を超えるときの n を求めます。n は整数なので、1から順番に+1ずつ入力して、答えを求めるのが一番簡単です。

ただ、このやり方は、数学的ではありません。どちらかというと計算機的発想です。計算機は、繰り返し計算は非常に得意です。特に精度を気にせずできる方法ではその方が確実に正解に近づきます。

数学的に求めるなら、数式を変形させて、

と対数計算をさせれば、一回計算されれば答えがでるはずですが対数計算は精度が落ちます。Pythonがどうなっているのか不明ですが、浮動小数点演算には、精度桁数があり、対数計算ではその桁数が精度に影響します。精度に影響がでないように対数計算をさせることをやっている可能性も大いにありますが、一応両方のパターンでやってみましょう。

といっても大したプログラムではありません。

まだ、Python触ったばかりなのでご容赦ください。

ほぼ説明はいらないかと思いますが、ちょっと引っかかったのは、型変換float()を使うところでしょうか。

pythonは型を意識しているのかいないのか良くわからないのですが、適度にfloat()にしないとエラーになってしまいます。

文字として認識するのか整数なのかは比較的緩いのですが、小数演算が必要なところでは、float()が求められます。ちなみに、pythonのfloatは、C言語のdouble相当らしいです。

上記のコードをgacha.pyで保存してからコンソールから、python gacha.py で実行できます。

IDLE (Python 3.8 32-bit)を使ってソースを書いてるときは、[Run]>[Run Module] もしくは、F5キーを入力でも実行可能です。

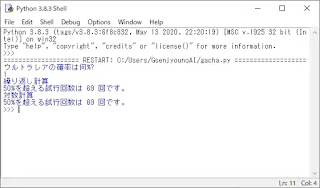
実行結果はこんな感じです。

入力値検証をしてないので、数字以外を入れるとエラーになります。手抜きプログラムです。

で計算結果は、50%を超えるまで繰り返すでも対数関数で一発計算でもほとんど差はないですね。対数計算は、math ライブラリをインポートしないと使えませんが、その差だけです。コードを短くするなら、対数計算の方がいいかもくらいな差ですね。

とりあえず、第一歩目なので、これから頑張って学んでいきたいと思います。次回は、これをGUI化してみたいと思います。